PEMDAS – What’s In A Name

In the arena of equation calculation, PEMDAS is the name of the game. The acronym PEMDAS, which stands for Parentheses, Exponents, Multiplication, Division, Addition, Subtraction, defines the order in which the components of a complex equation are completed. Its purpose is to allow equations to be consistently solved correctly.  Stray from the PEMDAS path and you’ll find yourself lost in the bog of error. A fatal misstep, especially if you’re trying to tout your math prowess on a site like Facebook, where tricky little equations are quite popular.  

The “parentheses” portion of PEMDAS is particular to the US. In other English speaking countries, “brackets” is the preferred term. This changes the acronym to BEMDAS.  Common terminology creates other variations in the acronym as well. For example, when using the term Indices in place of Exponents, the acronym becomes BIMDAS. The acronym GEMS is a short, sweet variation of PEMDAS that breaks the order of operations into 4 concise steps – Grouping Symbols (parentheses, brackets, etc), Exponents, Multiplication/Division (from left to right), Subtraction/Addition (from left to right).

Other variations come from the order of operations itself. In equation calculation, multiplication and division have equal weight, as do addition and subtraction. For consistency, therefore, these functions are completed working from left to right. 

If multiplication appears first, PEMDAS is correct. If division appears first, it would be PEDMAS.

Then there is BODMAS. The most commonly used acronym outside the US, it changes both the P and E of PEMDAS to B for Brackets and O for Order, and reverses the order of the multiplication and division functions.

Whichever variation you choose, PEMDAS and its acronym cousins will keep you on the path to success. Accurate navigation of the order of operations depends upon it.

PEMDAS – Order Is Everything       

Whether you use PEMDAS or any of its variations, the order of operations remains the same.        

•  1.  Parentheses or Brackets  ( ) [  ] – any functions within the grouping symbols are always calculated first. If the equation has more than one parenthetical calculation, begin with the innermost and work outward. Once a parenthetical calculation has been reduced to a single number, the parentheses can be removed.

3 + (12 ÷ 3) x 4 =                                   2x { 1 + [ 4x(2+1) + 3]} =

3 + 4 x 4 =                                              2x { 1 + [ 4x(3) + 3]} =

3 + 16 = 19                                             2x { 1 + [ 12 + 3]} =

                                                            2x { 1 +  15} =

                                                            2 x 16 = 32

• 2.  Order, Index, or Exponent  ² – These terms indicate operations containing powers or indices. All calculations in this category, like squaring or calculating square root, are performed following functions within parentheses.

(6 + 3) ² - 8 ÷ 4 x 3 =

9² - 2 x 3 =

81 – 6 = 75

• 3/4.  Multiply and/or Divide  X / ÷  – Since these functions have equal weight, they are calculated as third level of operations. When two or more of these functions appear in sequence, they are calculated from left to right.

                                                            2 + 3 x 4 =                                               20 ÷ 4 – 2 x 3 + 8 =

                                                            2 + 12 = 14                                           20 ÷ 4 = 5      2 x 3 = 6

                                                                                                                             5 – 6 = -1

                                                                                                                             -1 + 8 = 7

• 5/6.  Add and/or Subtract   + / -  – These functions also carry equal weight, so they are also calculated in sequence from left to right after all other functions have been completed.

6 – (5 – 3) + 10 =                    4 x 3 – 9 + 3 x 5 =

 6 – 2 + 10 =                                12 – 9 + 15 =

     4 + 10 = 14                                   3 + 15 = 18

And that, my friends, is the order of operations. While there are no exceptions to the PEMDAS rule, there are, however, two special cases involving exponents that should be mentioned here. 

First, when an exponent is included as part of a parenthetical group, the exponent takes precedence over everything else.

The second is a little more complicated.  When there is an exponent with its own exponent, the equation is calculated from right to left first, then from left to right. For example, 8²² would be calculated as 8 to the power of 2 squared, not as 8 to the power of 22. In this case, the first step is to calculate the square of 2, which is 4. This gives us the number of times that 8 must be multiplied. Since 8 is also the base number it would be expressed as 8 to the power of 1. From there, PEMDAS kicks in and 8 is multiplied 3 more times, using the sum of the previous calculation as the multiplier.    

                                                                        1 x 8 = 8              (8 to the power of 1) 

                                                                        8 x 8 = 64            (8 to the power of 2)

                                                                        64 x 8 = 512        (8 to the power of 3)

                                                                        512 x 8 = 4,096   (8 to the power of 4)          

One final piece of advice. It is the P of PEMDAS (Parentheses) that is your navigational guide along the path of equation calculation. Use it as you would a road map. Reading that map correctly is crucial to reaching your destination successfully.

PEMDAS And You   

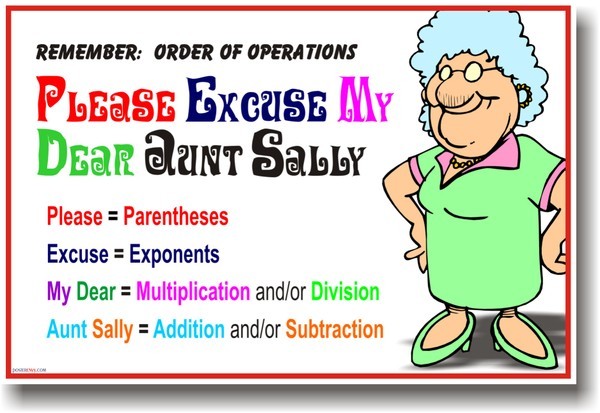
Having a problem remembering PEMDAS? A mnemonic, a type of memory aid, may help.  The most commonly used mnemonic for PEMDAS is “Please Excuse My Dear Aunt Sally.” And with that, we’re turning you loose. Now it’s time for you to embark on a PEMDAS journey of your own, so pack up Aunt Sally and hit the road to equation calculation.  Here are a few warm-up exercises to get you started:

3 + 4 x 2 = ?   9, 10, 11, or 14      3 + 3 x 3 – 3 + 3 = ?   18, 12, 3, or 6       6 ÷ 2 x (1 + 2) = ?   9 or 1      48 ÷ 2 x (9 + 3) = ?   2 or 288    

OK. Feeling a little more confident? Try these:

25 – 55 + (85 + 65) = ?            6 x (4+15) – [7 x (56 – 19)] = ?            60 ÷ (24 ÷2) x 4² +25 = ?

You’re on a roll now. Better get Aunt Sally and your calculator for this trio:

7² + 5 x 8 +6 ÷ 6 – 12 x 2 – (12 – 4) = ?            2² x [14 – (6 + 3)] ÷ 10 + 16 – 2 = ?      and, just for fun,      100 + (34 – (4 + 2) x 3) = ?                                                                                                                                                                                    4

Finally, you’re ready for those Facebook favorites:

7 + 7 ÷ 7 + 7 x 7 – 7 = ?       1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 0 x 1 + 1 = ?        4 x 4 + 4 x 4 – 4 x 4 = ?           7 – 1 x 0 + 3 ÷ 3 = ?

To continue your PEMDAS journey, you’ll need a top notch calculator companion.  If your current calculator is not equipped for road trips like this, check out SellYourCalculators.com. We offer competitive prices for calculators that can’t cover the necessary ground, and our quick turn-around time and outstanding customer service will have you “wowing” the Facebook crowd faster than you can say “Please Excuse My Dear Aunt Sally”. Contact us today for more information about our calculator buyback program.